Links The Human Music Memory Map The Groove Project Musical Spaces Templeton Advanced Research Program

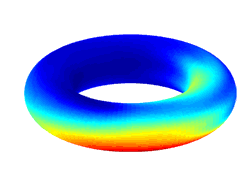
Beyond the Beat: modeling metric structure in music and performance
links- Download: BTB is available for download as part of the Janata Lab Music Toolbox (jlmt). Please visit the jlmt page for more information and to download this package.
- Detailed information on this project can be found in the following article:
Tomic, S. T., Janata, P. (2008). Beyond the beat: Modeling metric structure in music and performance. J. Acoust. Soc. Am. 124(6): 4024-4041. - Getting in "the groove" while tapping - Poster presented at Society for Music Perception and Cognition (SMPC), 2007.
- Janata, P., Tomic, S. T., & Haberman, J. (in press). Sensorimotor coupling in music and the psychology of the groove. Journal of Experimental Psychology: General.
Beyond the Beat (BTB) is an algorithm for analyzing timing characteristics of musical signals. It provides a framework that allows one to ask questions about the presence and relative prominence of different metric levels and rhythmic patterns in musical recordings. BTB draws from the work of Scheirer (1998) and Klapuri et al. (2006), two models that were developed primarily for the purpose of beat estimation. The most significant difference between BTB and these two models is the employment of reson filters instead of comb filters for the inspection of periodicities of the onset pattern in the signal. Reson filters behave like damped oscillators and may be better suited for extracting multiple metric levels from musical acoustic signals. BTB resembles the model by Large (2000), who employs a network of Hopf oscillators and includes similar preprocessing steps, such as the incorporation of an auditory periphery model. Active oscillators in his model actively inhibit other oscillators, however, while the reson filters in BTB do not have this interaction.
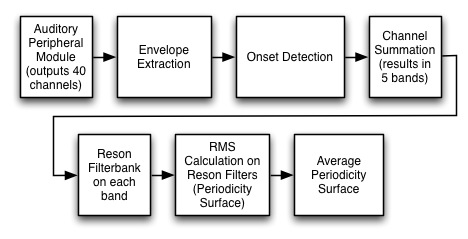
Our model was written in Matlab. The following figure schematizes the processing steps. First, we pass the audio signal through the Auditory Peripheral Module of the IPEM Toolbox. The output of the module is an auditory nerve image (ANI), which represents the auditory information stream along the VIIIth cranial nerve. The output results in 40 channels of data. Next, we extract the amplitude envelopes by performing an RMS calculation on the output of each channel. Onset patterns are then extracted by a difference calculation and half-wave rectification. We then sum every 8 adjacent channels to produce five bands. Each of the five bands is passed through a bank of reson filters. An RMS calculation is performed on each band to facilitate the identification of the relative amplitudes of each filter. We refer to the surface plot of the RMS of each band as a periodicity surface. The 5 bands are then combined into an average periodicity surface (APS).
examples
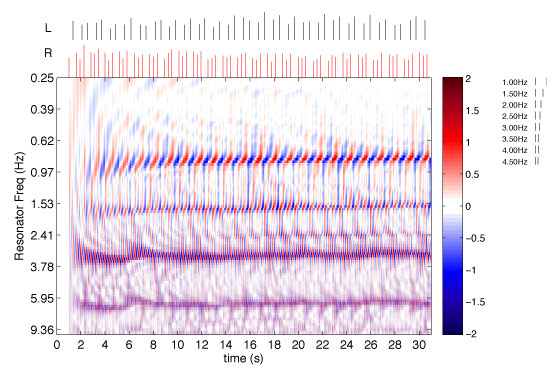
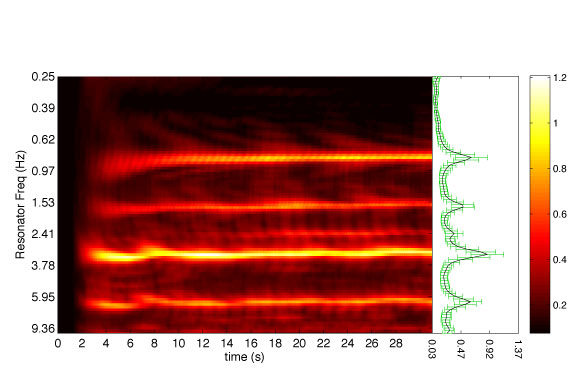
Below are example excerpts of commercial musical recordings retrieved from the iTunes Store previews, available for free to the public prior to making a purchase. The excerpts were processed with BTB and the resulting APSs and MPPs are illustrated. The APSs illustrate how the metric structure of the excerpts change over time while the MPPs (on the right adjacent side of the APSs) illustrate the average metric heirarchy over the course of the excerpt. The black line of each MPP plots the mean of the APS over time while the green bars plot the standard deviation.
| "If I Ain't Got You" by Alicia Keys | |
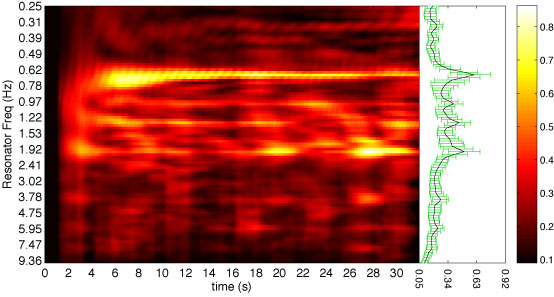
| |
| "Maiden Voyage" by Herbie Hancock | |
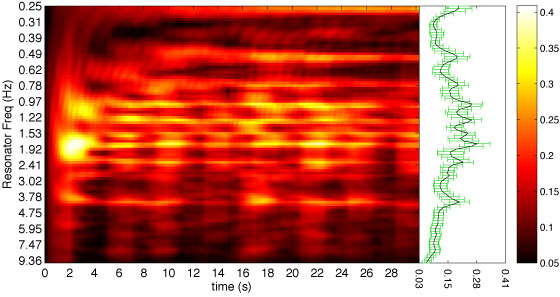
| |
| "Hymn for Jaco" by Adrian Legg | |
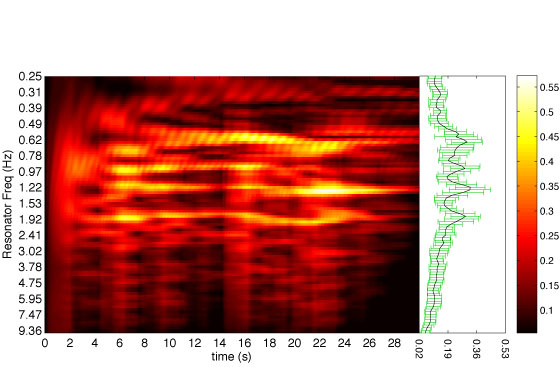
| |
| "It's a Wrap (Bye, Bye)" by FH1 (Funky Hobo #1) | |
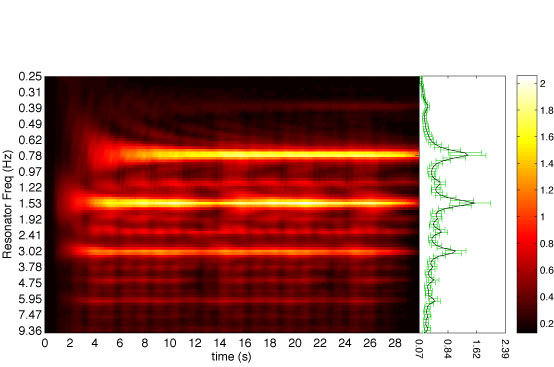
| |
Alternately, one could use BTB to process MIDI inputs. In this case, it isn't appropriate to process the data through portions of the model concerned with simulating the auditory nerve firing rate and onset pattern extraction. Instead, we convert each note on message into a Dirac impulse. The signal produced in this fashion is then passed directly into a single resonator bank in order to produce periodicity surfaces and MPPs. Currently, for bimanual tasks, we do not differentiate between left and right hand taps. The amplitude of each Dirac impulse is linearly scaled by calculating the ratio of the note's MIDI velocity to the maximum velocity.
|
|
BTB was developed by Stefan Tomic and Petr Janata.
We would like to thank Peter Keller and Bradley Vines for their comments and suggestions. We are also indebted to Peter Keller, Joe Saavedra, and Philip Front for developing the Max/MSP patch for constructing the percussion patterns used in this study and to Rawi Nanakul for the collection of tapping data. This work was supported in part by a Templeton Advanced Research Program grant from the Metanexus Institute to P.J.
References- Klapuri, A. P., Eronen, A. J. and Astola, J. T. (2006). "Analysis of the meter of acoustic musical signals," IEEE Transactions on Audio Speech and Language Processing 14 (1), 342-355.
- Large, E. W. (2000). "On synchronizing movements to music," Human Movement Science 19 (4), 527-566.
- Scheirer, E. D. (1998). "Tempo and beat analysis of acoustic musical signals," J. Acoust. Soc. Am. 103 (1), 588-601.